本文共 3516 字,大约阅读时间需要 11 分钟。
本文邀请谷歌开发者专家彭靖田为大家系统整理了10个学好 TensorFlow 2.2 的理由,帮助机器学习新手快速入门,并为开发者们提供对 TensorFlow 及其生态的全面认知。
接下来有请嘉宾——彭靖田

大家好,作为一路陪伴和见证 TensorFlow 从 v0.7 到现在的开发者和老用户,很开心有机会能够作为第一期嘉宾参与 TensorFlow “码上作答” 栏目,与各位分享我对 AI / TensorFlow 2.2 的学习经验和心得体会。
这一期,我想尽可能系统化的谈谈对最新版本 TensorFlow 2.2 的看法。希望通过我整理总结的 10 个学好 TensorFlow 2.2 的理由,AI 新玩家们可以快速入门,TensorFlow 老师傅们能够获得一个更加全面的视角来认知 TensorFlow 及其生态。
理由1:快速上手只需十分钟
TensorFlow 2.2 在易用性和简化 API 方面做了大量优化。对于新手,可以使用高层封装的 API 实现面向模型编程 ( Model Oriented Programming, MOP )。我们以一个典型的 MNIST CNN 模型为例,展示 TensorFlow 2.2 的实现:
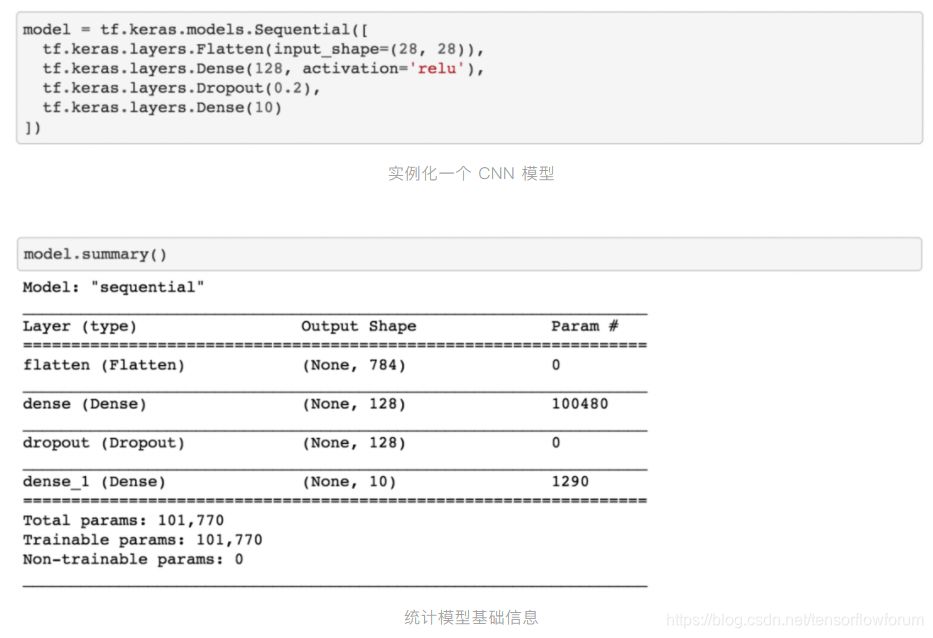
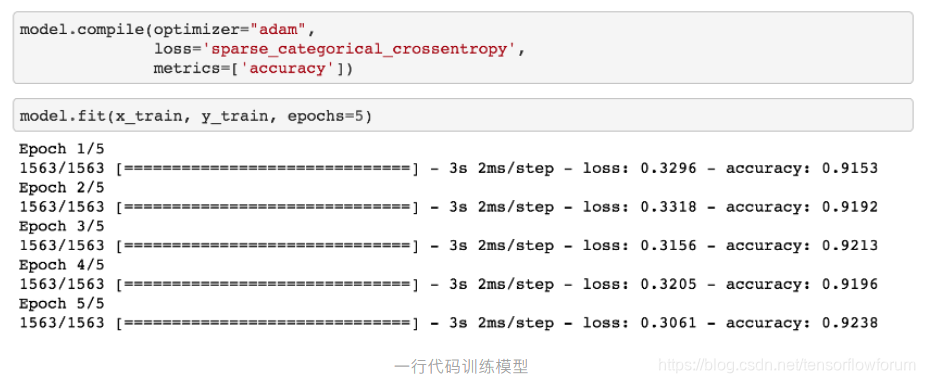
通过这个简单示例,我们得以管中窥豹。tf.keras 提供了一套面向模型的编程方法:实例化 ( Sequential 和 Functional API ) 、统计 ( Summary )、定义优化器和损失函数 ( Compile )、模型训练 ( Fit )、评估 ( Evaluate )、预测 ( Predict )、保存 ( Save ) 和加载 ( Load ) 等。这使得 TensorFlow 用户可以更加专注于模型开发和测试。
理由2:快速迁移现成 Keras 项目
TensorFlow 2.2 实现了 Keras 所有接口的完全兼容,并且解决了原生 Keras 不支持分布式训练的问题。
因此,如果你已经在使用 ,可以尝试使用 import tensorflow.keras as keras来进行快速迁移。如果你想要尝试扩展 Keras 分布式训练,也可以使用 tf.distribute 模块赋能你之前的训练代码。
理由3:快速部署生产环境
很多老用户都对 TF Serving 这款生产级的 AI 服务框架赞不绝口。TensorFlow 2.2 不仅发扬了前辈的优良传统,同时将 tf.keras 训练的 HDF5 模型格式和 SavedModel 格式打通。你可以在使用 (“saved_model”) 保存模型时选择 TF Serving 可加载的 SavedModel 目录。接着,你只需要使用 TensorFlow Serving 官方镜像 tensorflow/serving 便可以快速将 AI 模型部署到生产环境。
理由4:快速实现模型分布式训练
TensorFlow 早在 v0.8 就已实现基于 PS-Worker 的分布式模型训练。
经过3年多的迭代和更新,TensorFlow 2.2 不仅提升了的性能,而且通过内置的6种分布式训练策略,帮助不熟悉分布式计算的新同学用一行代码实现分布式训练,效率提升十分明显。

理由5:原生支持多元化的数据处理
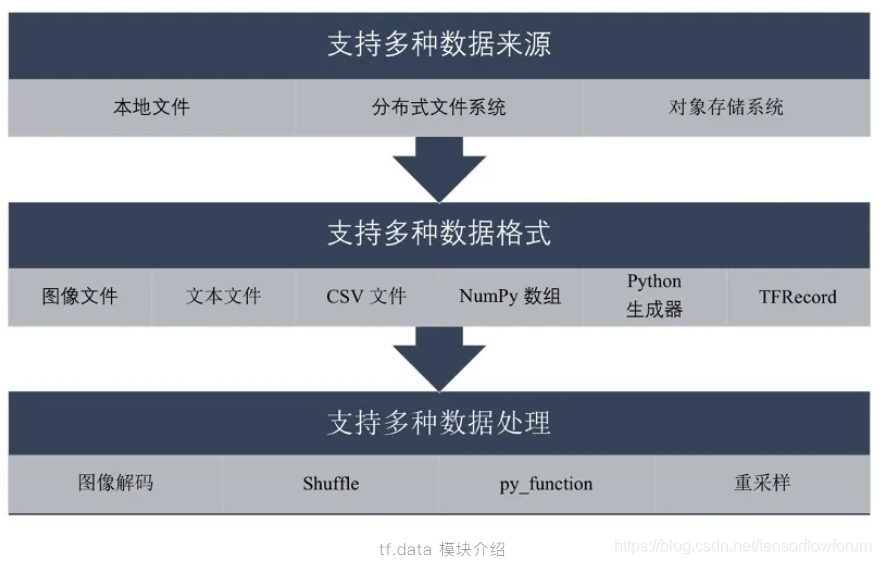
是 TensorFlow 2.2 推荐使用的数据处理 API ,其强大的功能体现在对于多种数据来源、数据格式和数据处理方法的支持。对于个人开发者和小团队,可以使用本地文件和对象存储系统作为数据来源,对于拥有海量数据的大厂,则可以从分布式文件系统中分批次读取数据或搭建数据处理流水线。
从数据格式和内置数据处理方法的丰富度上,我们可以洞察到 TensorFlow 2.2 已不仅是一个处理计算机视觉或深度学习的框架,而是能够实现 NLP 和 GAN 等多种细分 AI 领域的通用 AI 框架。
理由6:原生支持经典分类模型
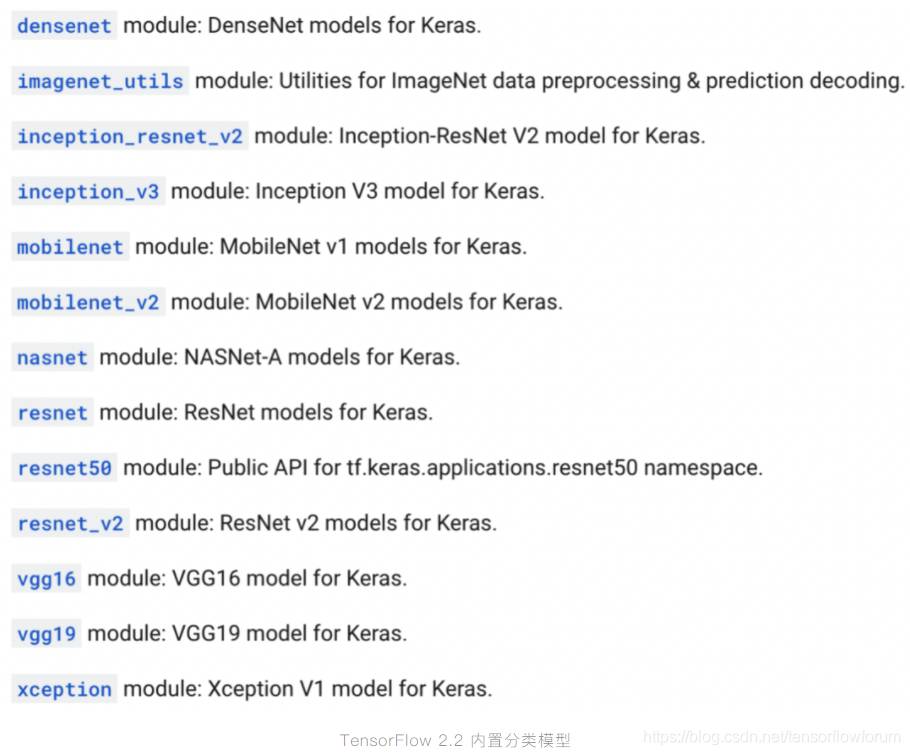
TensorFlow 2.2 原生支持了多种经典分类模型,包括重量级的 EfficientNet(最新 nightly 已支持)、DenseNet、 ResNet、VGGNet 和轻量级的 MobileNet、Xception 等。你可以通过 模块快速体验和使用这些经典模型。不论是在基于 ImageNet 上预训练的模型做迁移学习,亦或是从零到一的训练全新模型。
理由7:原生支持移动和物联网设备
在 TensorFlow 1.x 时代,SavedModel 转 tflite 格式部署到移动和物联网设备是可行的,但易用性不算很好。
TensorFlow 2.2 将 TF Lite 生态进一步整合到了原生框架中,并正式推出了 模块。现在,你可以直接调用 tf.lite.TFLiteConverter 实现 SavedModel、HDF5 和 ConcreteFunctions 等多种模型格式转 tflite 格式。

同时,你还可以通过 tf.lite.Interpreter 定义模型在物联网设备上运行时的预测接口。这使得 TensorFlow 2.2 真正实现框架原生支持 AIoT。
理由8:原生支持可视化数据、模型和训练
在深度学习模型训练和评估过程中,海量数据、高维模型、多种指标的变化对于算法工程师来说是十分重要的信息。并且,如果能够有高效的手段获取其中的数据洞察,将会非常有助于提升模型训练效率和经验积累。
TensorBoard 可视化工具包自推出后一直广受好评,它的出现使得开发者能够更加直观的了解数据和模型的质量,以及关键指标分布和变化。在今年的 TensorFlow Dev Summit 上,官方团队发布了 在线版 ()。这使得 TensorFlow 用户不再需要独立安装 TensorBoard,而能够直接体验到 TensorFlow 生态中这一重要特性。

理由9:前沿探索量子机器学习
量子机器学习 (QML) 是量子信息 (Quantum Information) 领域内新兴的子领域,其将量子计算的速度与机器学习所提供的学习和适应能力结合到了一起。量子机器学习可以分为两个部分:
将从量子计算机和传统计算机获得的数据作为训练数据训练模型的机器学习算法。 过量子力学的思想和模型来改进机器学习算法也属于量子机器学习的一部分。量子机器学习自1988年首次提出细胞自动机的量子推广后,逐步发展出量子增强学习 (2008) 、HHL 量子算法 (2009) 、量子主成分分析 (2014) 、量子 SVM 和贝叶斯网络上的量子推断 (2014) 、量子推荐系统 (2016) 等经典算法的拓展。
虽然现阶段量子计算机和量子比特数量限制还无法大规模使用 QML,但作为最前沿的交叉学科,TensorFlow 2.2 也实现了对这一前沿领域的支持—— 。

理由10:企业版助力数字化转型
许多企业用户对于 TensorFlow 快速发展带来的 API 版本变化想必是心有余悸。一个好消息是此类用户将由官方团队“兜底”。 将提供长期的技术支持。
针对某些版本,谷歌将提供长达三年的补丁程序,所有补丁和错误修复将在 TensorFlow 主线代码存储库中提供。另外,谷歌还将向正在构建 AI 模型的公司提供来自 Google Cloud 和 TensorFlow 团队的工程协助。
One More Thing
我希望不论是从业者,亦或是有志于投身 AI 的新同学,都能够勇敢踏出学习 AI 的第一步:快速上手一个 AI 框架—— TensorFlow 2.2 。同时,在 AI 理论积累和动手实战的基础上,持之以恒地学习,逐渐成长为一个玩转 AI 技术的 TFBoys / TFGirls 。
最后,打个小广告:为了系统化和全方面的分享这几年在 AI 落地实战中积累的的踩坑经验和 TensorFlow 2.2 的使用技巧,我在极客时间开设了课程。
同时,课程中的项目实战代码也已 ,欢迎有兴趣的同学关注和订阅!
附录:
我为大家整理好了一系列学习资料,马上一键到达!
如果也想像大神一样快速进步,别错过 TensorFlow 官方团队在中国大学慕课平台推出的《TensorFlow 入门实操课程》,帮助你了解更多机器学习设计思路和实践模式。立即点击学习吧!
想了解更多大神的经验分享?扫码关注TensorFlow官方微信公众号( TensorFlow_official ),产品更新、课程教学、技术实践、应用实例等精彩内容一网打尽!

转载地址:http://upmz.baihongyu.com/